The Genius Myth
Are you a math person? I’ll bet you’ve decided one way or the other — or maybe a teacher or parent decided for you and you ran with it. It is common for people to decide if they’re “math people or if they’re not math people” at a very young age.1
But I’m here to tell you that that’s silly. We have a problem in math: the “genius myth.“2 Too many of us believe that “success requires some natural ability [or] unteachable qualities.”3 Luckily, it’s completely false.
Whether you believe you’re a math person or not a math person, you can study for math. If you’re struggling in math, it’s likely you’ve never learned how to study math — it’s different than studying ELA, History, or even Biology! And if you already consider yourself a math person, it’s a good idea to learn some math study strategies before you encounter a math problem that could change your mind!
The Four Step Formula to Study for Math
There are four essential steps to studying for math:
- Learning the theorems, equations, and methods that you’ll need.
- Learning how to use them.
- Learning how to know which one to use.
- Practice, practice, practice!
If you can learn to think of each step one at a time, you can make study guides that have everything you need without getting lost or overwhelmed.
This is the method I used throughout engineering school, and I got straight A’s!
Let’s look at each step in more detail.
1. Learning the Theorems and Equations that You’ll Need
The first step in studying for math is to find out what exactly you need to know. As you find this information, you’re going to make a list on a blank sheet of notebook paper. Depending on how your class is set up, there are a few places you might be able to find this information:
Textbook
If your class is following a textbook, that’s the perfect place to look. Go to the chapter(s) that you’re studying and write down every equation or theorem that you see. (These are usually set aside in a little box, or separated from the main text and bolded to make them easier to find).
Lecture Notes or Slides
If your class is not following a textbook, or if your class deviates a lot from the textbook, you may need to find equations and theorems in your class notes or in the lecture slides. Similarly to the textbook method, write down every equation or theorem that you see.
Homeworks and Practice Problems
Homeworks and practice problems are more difficult to use for finding information, since they’re not specifically made for this, but if you don’t have a textbook, good lecture notes, or access to lecture slides, you can find what you need in your homeworks or practice problems. To do this, you will need to identify which equation or theorem you used to solve each problem, and write those down. This might take some time, but it’s all time that you’re learning things, so it’s not a waste!
This is the last option for a reason: there is an overwhelming amount of information on Google, and it’s not tailored to your class. So it may be difficult to find the information that you actually need, or the information that you find may require you to learn extra things in order to understand it. If you have to Google something, go ahead, but try to use your other resources first!
2. Learning How to Use Your Equations and Theorems
Once you have your list of every equation and theorem you need to know, you need to make sure that you know how each one works.
For example, if we were studying for a Geometry unit on triangles, we might have the Pythagorean Theorem ( \(a^2 + b^2 = c^2\)) written down on our paper.
Does \(a^2 + b^2 = c^2\) mean anything to us? What is \(a^2\)? What is \(b^2\)? What is \(c^2\)? What can we even use this for? These are the questions that we now need to answer.
You can probably find this information wherever you found your equations and theorems, or if not, you can definitely find it online.
The most important thing is to define your variables: equations and theorems mean nothing if we don’t know what the variables represent!
In this case, \(a\) is the short leg of a right triangle, \(b\) is the long leg of a right triangle, and \(c\) is the hypotenuse of a right triangle. (If you don’t know what any of those words mean, you would at this point define those on your paper as well).
Your paper might now look like this:
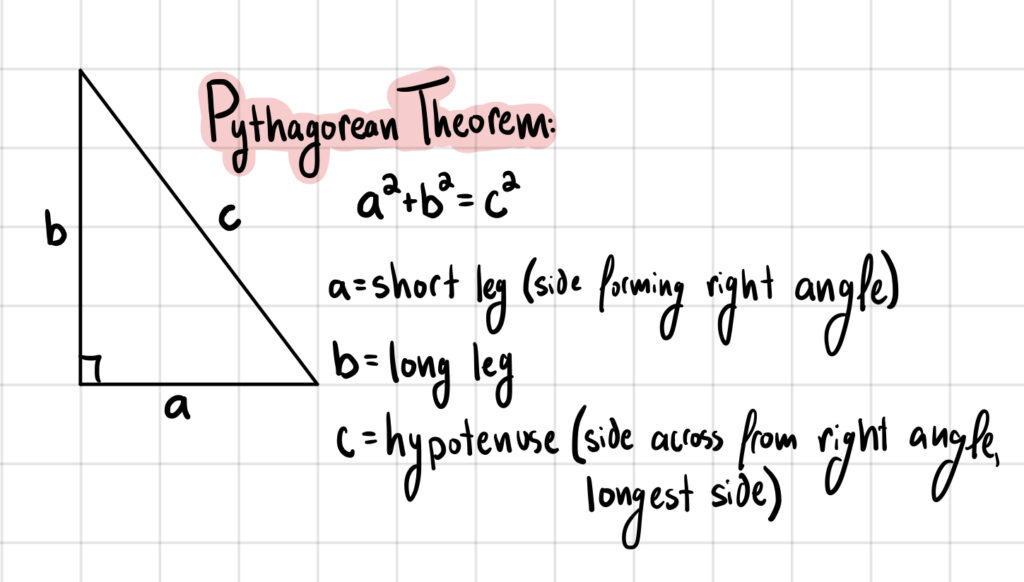
Once you’re satisfied with your information about one equation, theorem, or method, continue defining each equation, theorem, or method that you need to know.
Remember, this is for you. If you need a lot of information and definitions to help you feel confident, write them all down! If making it pretty helps you feel good about it, make it pretty!
3. Learning How to Know Which Theorem or Equation to Use
This is the step where people often get lost and decide that there are math people and not math people. Sometimes, it feels like “math people” are using math magic to decide which equation, theorem, or method to use for each problem.
Take factoring, for example. Most people are not confused by the individual factoring methods they learn in algebra. They are confused by looking at an equation and trying to decide which method to use. And admittedly, it can kind of feel like witchcraft!
But it’s not — there are clear rules to what you should try and in what order — we just often don’t learn or internalize those rules.
So what should you do here? I recommend the following:
- Look through your list of equations and theorems and write down what each one is specifically for.
- Make a flow chart. What are the questions you need to ask yourself to figure out which equation to use? In which order should you ask them? Once you’ve made the flow chart, you can use it as you practice. Chances are, once you’ve gone through all of the thinking required to make the flowchart, you’ll remember most of it without too much extra effort!
4. Practice, Practice, Practice!
Once you have your equations, theorems, and methods — and any information you need in order to use them (including your flowchart!) — all that’s left to do is practice.
Ideally, you want to practice on problems that have accessible answers or solutions so that you can check your work and figure out if you’ve got it or if you need revisit something.
You can get those problems from a few places:
Textbook
Your textbook is the perfect place to get practice problems. Most textbooks have answers for the odd problems and full solutions for some selected problems.
Graded Homeworks or Practice Problems
If you have homeworks or practice problems that your teacher or professor has graded or provided solutions for, those are ideal practice because they’re likely similar to the problems that will be on your test.
Lecture Notes or Slides
You can also try reworking any example problems from class. For these, try to do the problem without looking at your notes and then check your work.
Go Forth and Study Math!
Now that you’ve learned the process for studying math, it’s time to try it yourself!
If you feel yourself starting to panic and revisit the idea of “not being a math person,” take a few deep breaths, get a snack, take a walk, and then come back to studying armed with the knowledge that you can study and learn math — no pre-existing genius required!
- Mc-Dermott-Murphy, Caitlin. “The myth of the ‘math person’.” The Harvard Gazette, 9 November 2022, https://news.harvard.edu/gazette/story/2022/11/the-myth-of-the-math-person/. Accessed 17 February 2025. ↩︎
- McDermott-Murphy. ↩︎
- Mc-Dermott-Murphy. ↩︎
Leave a Reply